Note Taking Tips
As you get involved with the complexities of note taking, you may tend to forget the simple things that can make life a lot easier. These tips are little hints that we all know but forget sometimes. They can be summarized by four directives:
- BE ALERT – so you are aware of and prepared for the lecture content and situation.
- BE ORDERLY – so you can process the lecture now and for review later.
- BE SYSTEMATIC – so you can establish a habit pattern and won’t miss anything important.
- BE UP TO DATE – so that your well designed note taking system gets done.
Below is a list of tips which may help you to be alert, orderly, systematic, and up to date.
- Attend lectures regularly. Once you miss one, it will be easier to miss more.
- Use a standard 8 ½” x 11″ loose leaf notebook, for continued organization and review. Spiral notebooks do not allow reshuffling your notes for review.
- Keep the notes for one class separate from other classes. Best yet, keep each class in a separate binder.
- Write on one side of the paper for easier organization. It’s possible to overlook material written on the back of a sheet.
- Leave your notebook at home and carry with you only enough pages to keep track of the lecture. This way you won’t lose your entire set of notes should you misplace them.
- Carry extra pens and pencils for editing and unforeseen obstacles (UFO’s).
- Don’t doodle because it distracts. Keep eye contact when not writing.
- Make notes as complete as needed and as clear as possible so they can be used meaningfully later.
- Leave blanks where information is missed or misunderstood. Fill in gaps after lecture or as soon after as possible with the aid of the instructor or classmates.
- Develop your own system of enumerating and indenting.
- Use symbols such as asterisks for emphasis.
- Mark or separate assignments given in class in a space apart from the lecture notes.
- Separate your thoughts from those of the lecture; record your own items after the lecture.
- Be alert for cues, postural, visual, etc.
- Record examples where helpful.
- Listen especially at the end of the lecture. If the instructor has not paced his lecture well, he may cram half of the content into the last 5-10 minutes.
- Get into the five-minute technique and review your notes right after class. At this time you can change, organize, add, delete, summarize, or clarify misunderstandings.
- Recopying by itself is a debatable advantage but the five-minute technique is not.
- Have study sessions once or twice a week to learn omissions, clear up misinterpretations and get other students opinions about interpretations.
Works Cited
- Deese, James and Ellin K. Deese. How To Study (3rd ed). New York: McGraw-Hill, Inc., 1979.
- Johnson, Sue. The 4 T’s: Teacher/You, Text, Talk, Test – A Systematic Approach To Learning Success. California Polytechnic State University, San Luis Obispo.
- Pauk, Walter. How To Study In College (2nd Ed). Boston: Houghton Mifflin Co., 1974.
- Raygor, Alton L. and David Wark. Systems For Study. New York: McGraw- Hill, Inc, 1970.
Notetaking Systems
The Cornell Method
The Cornell method provides a systematic format for condensing and organizing notes without laborious recopying. After writing the notes in the main space, use the left-hand space to label each idea and detail with a key word or “cue.”
Method
Rule your paper with a 2 ½ inch margin on the left leaving a six-inch area on the right in which to make notes. During class, take down information in the six-inch area. When the instructor moves to a new point, skip a few lines. After class, complete phrases and sentences as much as possible. For every significant bit of information, write a cue in the left margin. To review, cover your notes with a card, leaving the cues exposed. Say the cue out loud, then say as much as you can of the material underneath the card. When you have said as much as you can, move the card and see if what you said matches what is written. If you can say it, you know it.
Advantages
Organized and systematic for recording and reviewing notes. Easy format for pulling out major concept and ideas. Simple and efficient. Saves time and effort. “Do-it-right-in-the-first-place” system.
Disadvantages
None
When to Use
In any lecture situation.
The Outlining Method
Dash or indented outlining is usually best except for some science classes such as physics or math.
- The information which is most general begins at the left with each more specific group of facts indented with spaces to the right.
- The relationships between the different parts is carried out through indenting.
- No numbers, letters, or Roman numerals are needed.
Method
Listening and then write in points in an organized pattern based on space indention. Place major points farthest to the left. Indent each more specific point to the right. Levels of importance will be indicated by distance away from the major point. Indention can be as simple as or as complex as labeling the indentations with Roman numerals or decimals. Markings are not necessary as space relationships will indicate the major/minor points.
Advantages
Well-organized system if done right. Outlining records content as well as relationships. It also reduces editing and is easy to review by turning main points into questions.
Disadvantages
Requires more thought in class for accurate organization. This system may not show relationships by sequence when needed. It doesn’t lend to diversity of a review attach for maximum learning and question application. This system cannot be used if the lecture is too fast.
When to Use
The outline format can be used if the lecture is presented in outline organization. This may be either deductive (regular outline) or inductive (reverse outline where minor points start building to a major point). Use this format when there is enough time in the lecture to think about and make organization decisions when they are needed. This format can be most effective when your notetaking skills are super sharp and you can handle the outlining regardless of the notetaking situation.
Example:
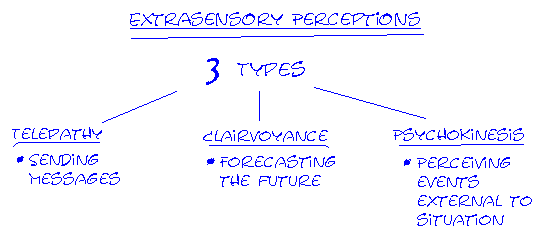
Extrasensory perception
-definition: means of perceiving without use of sense organs.
-three kinds –
-telepathy: sending messages
-clairvoyance: forecasting the future
-psychokinesis: perceiving events external to situation
-current status –
-no current research to support or refute
-few psychologists say impossible
-door open to future
The Mapping Method
Mapping is a method that uses comprehension/concentration skills and evolves in a notetaking form which relates each fact or idea to every other fact or idea. Mapping is a graphic representation of the content of a lecture. It is a method that maximizes active participation, affords immediate knowledge as to its understanding, and emphasizes critical thinking.
Advantages
This format helps you to visually track your lecture regardless of conditions. Little thinking is needed and relationships can easily be seen. It is also easy to edit your notes by adding numbers, marks, and color coding. Review will call for you to restructure thought processes which will force you to check understanding. Review by covering lines for memory drill and relationships. Main points can be written on flash or note cards and pieced together into a table or larger structure at a later date.
Disadvantages
You may not hear changes in content from major points to facts.
When to Use
Use when the lecture content is heavy and well-organized. May also be used effectively when you have a guest lecturer and have no idea how the lecture is going to be presented.
Example:
The Charting Method
If the lecture format is distinct (such as chronological), you may set up your paper by drawing columns and labeling appropriate headings in a table.
Method
Determine the categories to be covered in the lecture. Set up your paper in advance by columns headed by these categories. As you listen to the lecture, record information (words, phrases, main ideas, etc.) into the appropriate category.
Advantages
Helps you track conversation and dialogues where you would normally be confused and lose out on relevant content. Reduces amount of writing necessary. Provides easy review mechanism for both memorization of facts and study of comparisons and relationships.
Disadvantages
few disadvantages except learning how to use the system and locating the appropriate categories. You must be able to understand what’s happening in the lecture
When to Use
Test will focus on both facts and relationships. Content is heavy and presented fast. You want to reduce the amount of time you spend editing and reviewing at test time. You want to get an overview of the whole course on one big paper sequence.
Example:

The Sentence Method
Method
Write every new thought, fact or topic on a separate line, numbering as you progress.
Advantages
Slightly more organized than the paragraph. Gets more or all of the information. Thinking to tract content is still limited.
Disadvantages
Can’t determine major/minor points from the numbered sequence. Difficult to edit without having to rewrite by clustering points which are related. Difficult to review unless editing cleans up relationship.
When to Use
Use when the lecture is somewhat organized, but heavy with content which comes fast. You can hear the different points, but you don’t know how they fit together. The instructor tends to present in point fashion, but not in grouping such as “three related points.”
Three Examples:
Example 1:
A revolution is any occurrence that affects other aspects of life, such as economic life, social life, and so forth. Therefore revolutions cause change. (See page 29 to 30 in your text about this.)
Sample Notes:
Revolution – occurrence that affects other aspects of life: e.g., econ., socl., etc. C.f. text, pp. 29-30
Example 2:
Melville did not try to represent life as it really was. The language of Ahab, Starbuck, and Ishmael, for instance, was not that of real life.
Sample Notes:
Mel didn’t repr. life as was; e.g., lang. of Ahab, etc. not of real life.
Example 3:
At first, Freud tried conventional, physical methods of treatment such as giving baths, massages, rest cures, and similar aids. But when these failed, he tried techniques of hypnosis that he had seen used by Jean-Martin Charcot. Finally, he borrowed an idea from Jean Breuer and used direct verbal communication to get an unhypnotized patient to reveal unconscious thoughts.
Sample Notes:
Freud 1st — used phys. trtment; e.g., baths, etc. This fld. 2nd — used hypnosis (fr. Charcot) Finally — used dirct vrb. commun. (fr. Breuer) – got unhynop, patnt to reveal uncons. thoughts.
Bibliography
- Deese, James and Ellin K. Deese. How To Study (3rd ed). New York: McGraw-Hill, Inc., 1979.
- Johnson, Sue. The 4 T’s: Teacher/You, Text, Talk, Test – A Systematic Approach To Learning Success. California Polytechnic State University, San Luis Obispo.
- Pauk, Walter. How To Study In College (2nd Ed). Boston: Houghton Mifflin Co., 1974.
- Raygor, Alton L. and David Wark. Systems For Study. New York: McGraw- Hill, Inc, 1970.
